NumPy is one of the popular Python libraries. In this article, we’ll understand its usage with graphics and more practical approach. So you can visually relate and remember it.
Contents Sharing Conditions
All the images and contents used in this article are meant to be used on Solothought.com only. You can use it to make your personal note. But publishing it on any site, blog, video or other medium without a link to this site or article is prohibited.
1
import numpy as np

You can create numpy array by passing an array, or an array of array for multi-dimension array. It supports many formats.
1
2
3
4
5
6
np.array(list(range(4))) #array([0, 1, 2, 3])
np.array((0, 1, 2, 3)) #array([0, 1, 2, 3])
np.fromstring('1 4 ', sep=' ')
np.fromstring('1, 2', dtype=int, sep=',')
numpy.frombuffer(buffer, dtype = float, count = -1, offset = 0)
numpy.fromiter(iterable, dtype, count = -1) #from iterator
Some quick ways to create NumPy arrays are
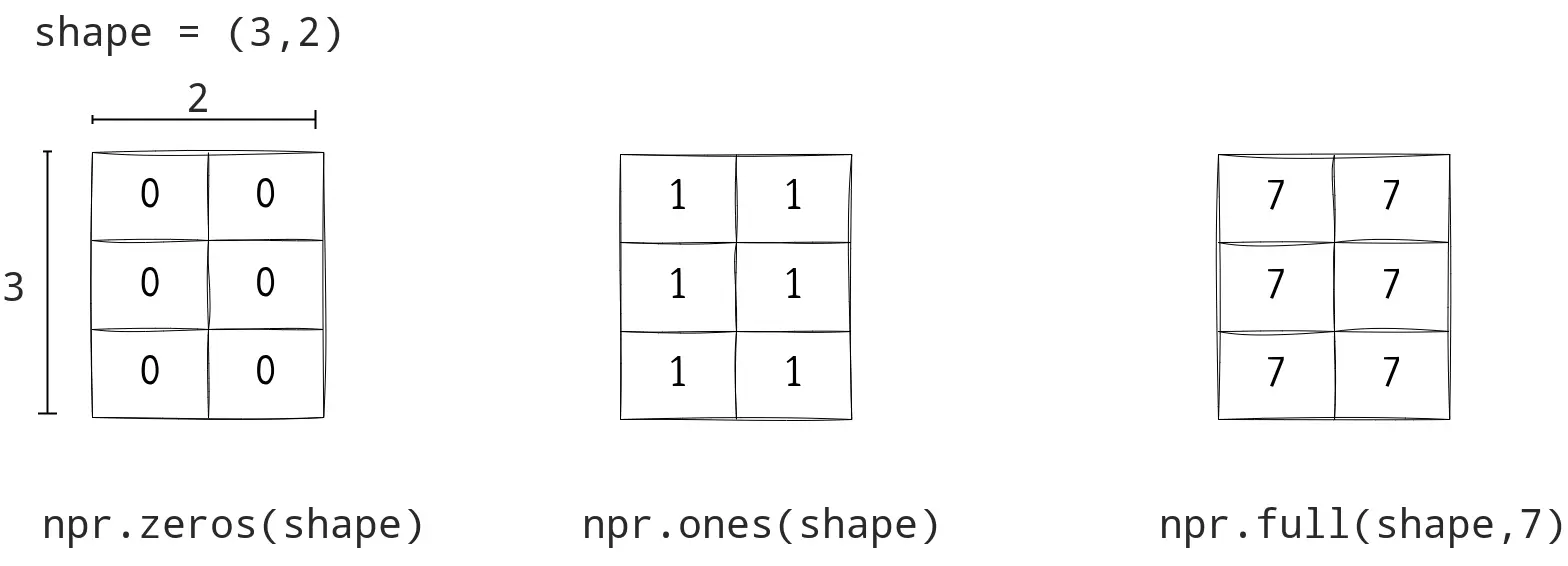
1
2
3
4
5
6
7
8
9
10
11
12
13
site = np.array([
[
["S","O","L","O"],["T","H","O","T"]
],
[
['.','c','o','m'],['b','l','o','g']
]
]);
site.shape # (2, 2, 4)
site.size # 16
site.ndim # 3
len(site) # 2
You can also create an array with random values
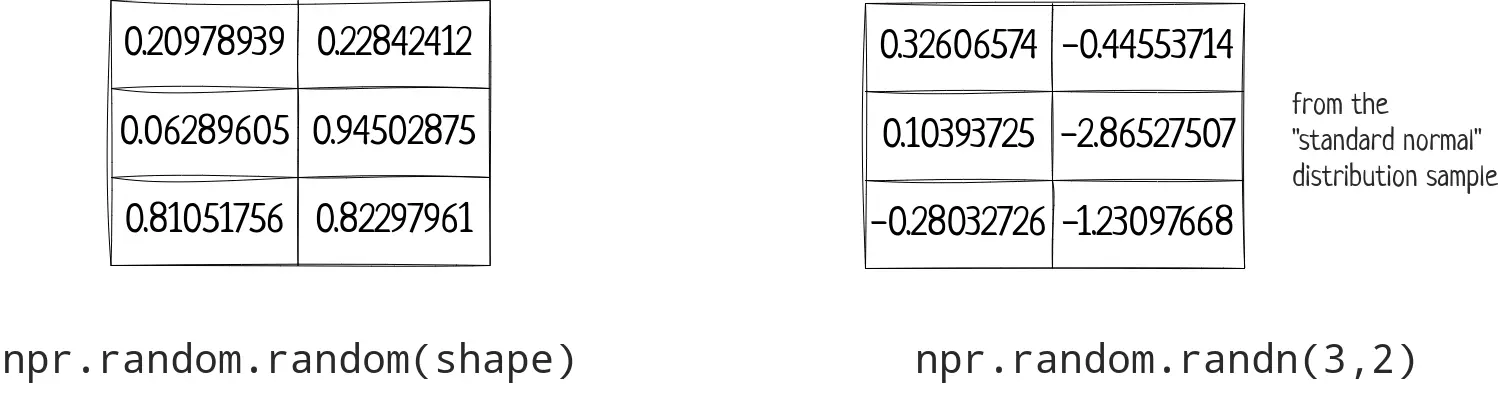
Some more functions
- arange: (a range) To create NumPy array.
np.arange(from ,to(not included), step)
1
2
3
4
5
6
7
np.arange(1 ,15, 2) #array([ 1, 3, 5, 7, 9, 11, 13])
a = np.arange(1,17).reshape(4,4)
a
# array([[ 1, 2, 3, 4],
# [ 5, 6, 7, 8],
# [ 9, 10, 11, 12],
# [13, 14, 15, 16]])
Arithmetic Operations

1
np.array((1,2,3,4)) - 1 # array([0, 1, 2, 3])
You can apply the other operations in the same way. However, remember that the right side array shape should be acceptable. This is also called Broadcasting.

1
2
3
4
5
6
7
A(2-D array): 4 x 3
B(1-D array): 3
Result : 4 x 3
A(4-D array): 7 x 1 x 6 x 1
B(3-D array): 3 x 1 x 5
Result : 7 x 3 x 6 x 5
Other operations
1
2
3
4
5
np.subtract(a, b) #or a - b
np.add(a, b) #or a + b
np.divide(a, b) #or a / b
np.multiply(a, b) #or a * b
a.dot(b) #dot product between a,b
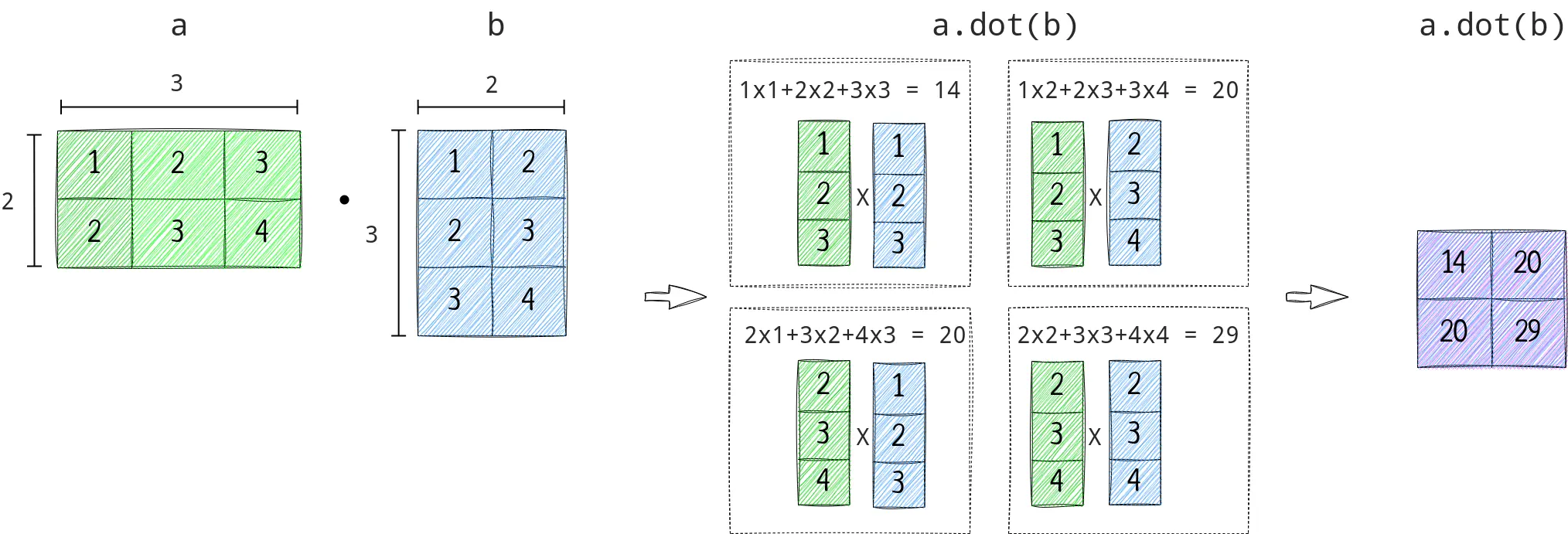
You can also perform many math operations on all the elements of NumPy;
1
2
3
4
5
np.exp(a) #Exponentiation
np.sqrt(a) #Square root
np.sin(a)
np.cos(a)
np.log(a)
Selection
To access an emelement from the array, you can use following patterns;
- arr[from:to:step] - To create another array from the original array.
- If
fromis not specified, it means 0 - If
tois not specified, it means length of that dimension - If
stepis not specified, it means 1
- If
- arr[at] - To select an elemnt at specific index
- arr[:] - all the elements of that dimension.
- arr[…] - all the elements of that dimension.
arr[:]means from start to end with step 1.arr[::]also mean the same.
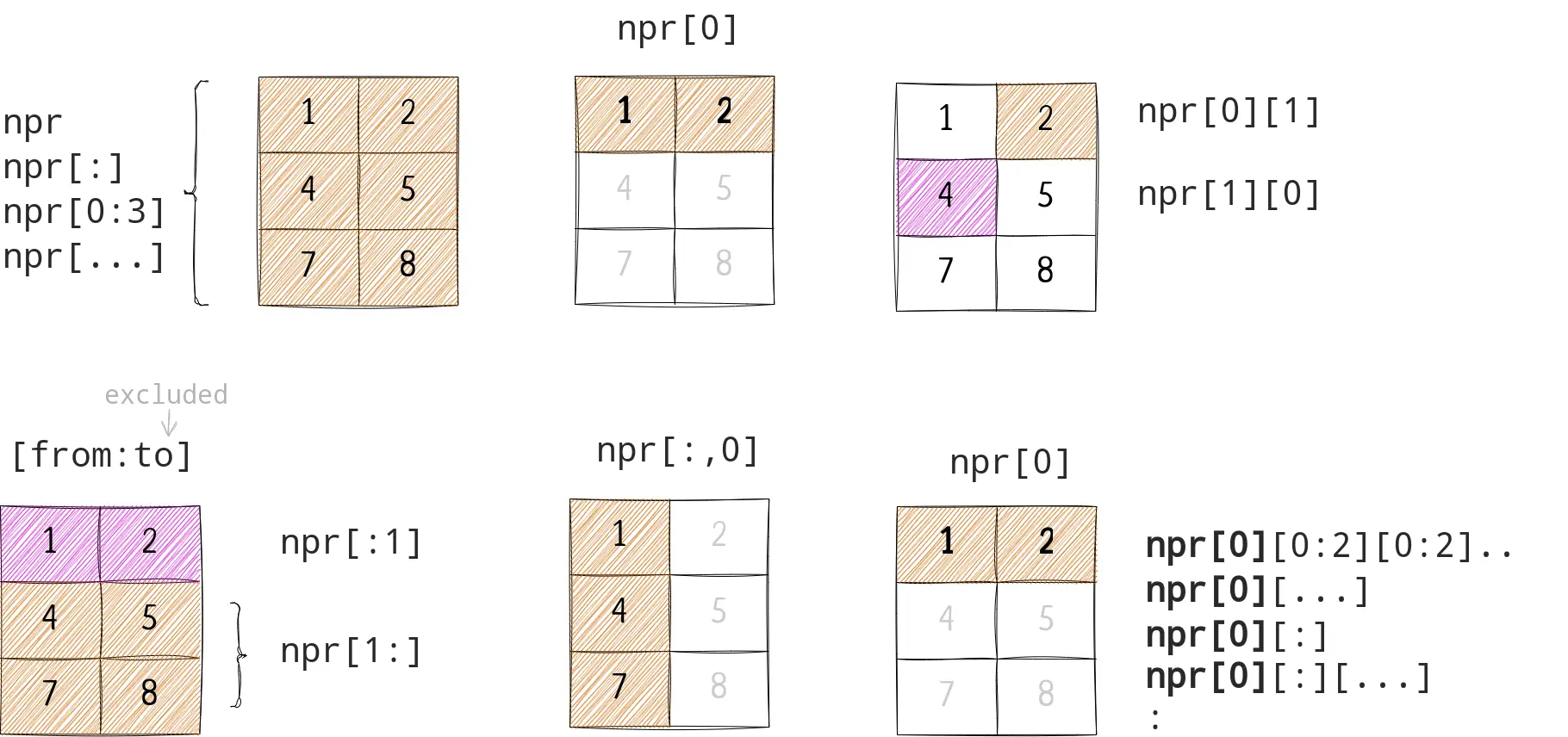
Isn’t it confusing that we can use multiple different expressions to select the same data from an array? Let’s understand why and how with examples.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
site = np.array([
[
["S","O","L","O"],["T","H","O","T"]
],
[
['.', 'c', 'o', 'm'], ['b', 'l', 'o', 'g']
]
]);
# All below expressions result ['T', 'H', 'O', 'T']
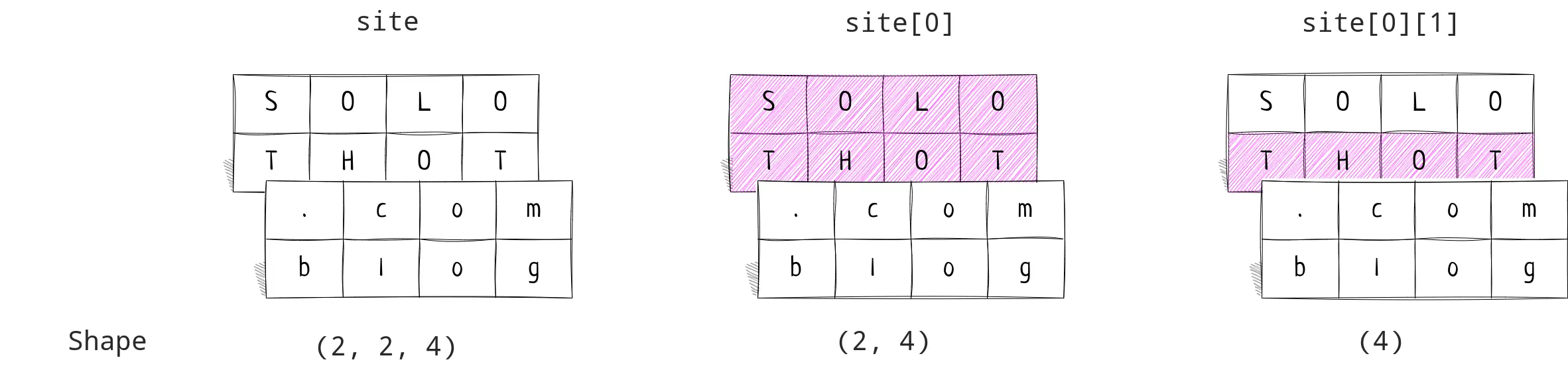
site[0][1]
site[0:1][0][1]
site[0:2][0][1]
# All below expressions result [['T', 'H', 'O', 'T']]
site[0:1,1]
Did you understand the difference between site[0][1] and site[0:1,1]?
In case of site[0:1,1], we first create a new NumPy array then select it’s 2nd element.
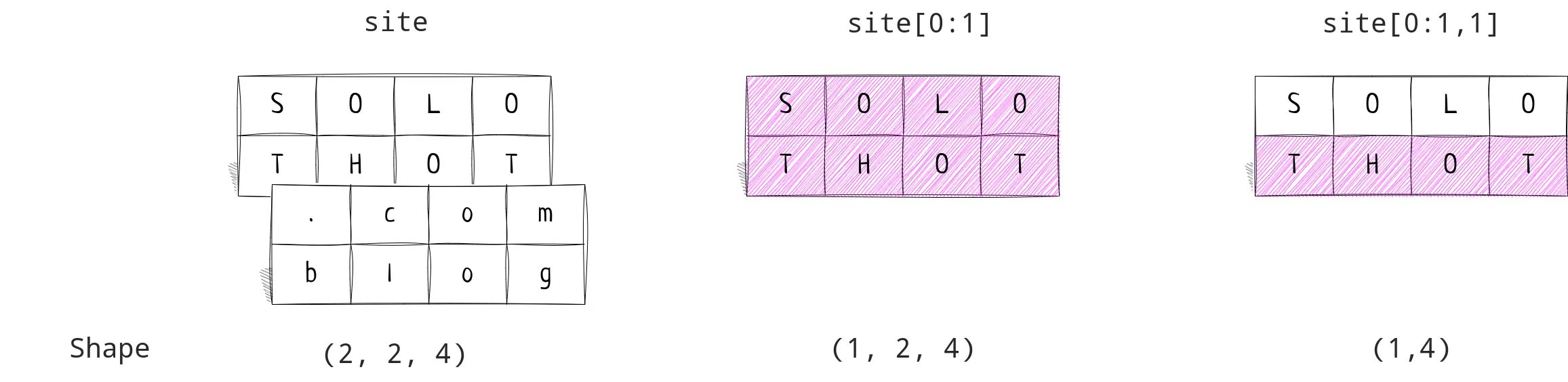
In case of site[0,1], we just refer the 2nd column of 1st element and return it.
Negative index and direction
Nump array indexing work in the same way of python native lists. You can use negative step to reverse the list, or a negative index to select an item from reverse direction.

1
2
3
4
5
6
7
8
9
site = np.array([
[
["S","O","L","O"],["T","H","O","T"]
],
[
['.', 'c', 'o', 'm'], ['b', 'l', 'o', 'g']
]
]);
site[:,:,::-1]
Output
1
2
3
4
5
array([[['O', 'L', 'O', 'S'],
['T', 'O', 'H', 'T']],
[['m', 'o', 'c', '.'],
['g', 'o', 'l', 'b']]], dtype='<U1')
Aggregation
NumPy provides direct function to perform an aggregation opperation and return the result.
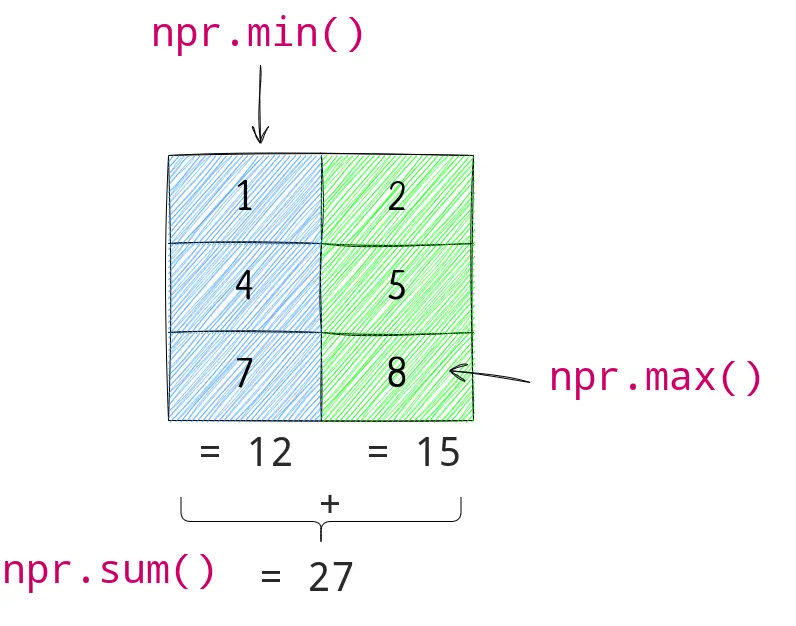
| fn | Description |
|---|---|
| a.sum() | sum |
| a.min() | min |
| a.max() | max |
| a.cumsum() | Cumulative sum |
| a.mean() | Mean |
| a.median() | Median |
| a.corrcoef() | Correlation coefficient |
| np.std(a) | Standard deviation |
Axis
You can perform aggregation on particular dimension as well.
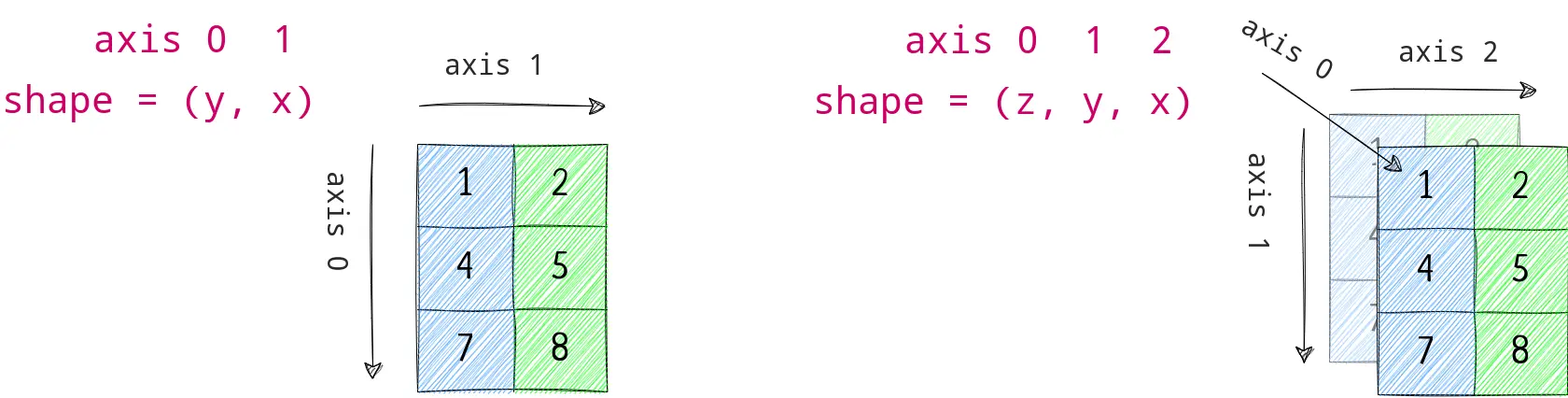
For a 3d array, there are 3 axis. When you select a particular axis, an operation is performed that axis-wise.
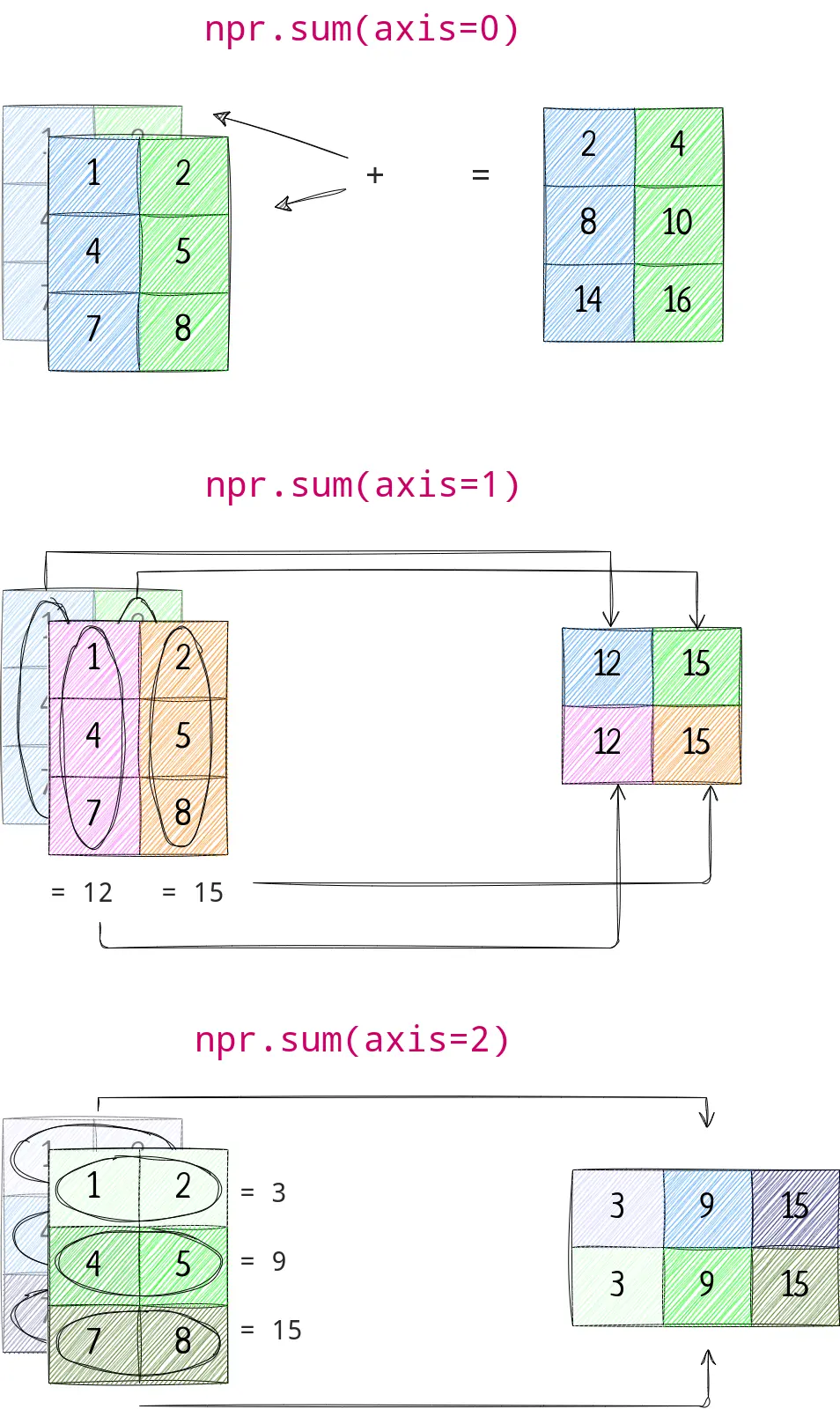
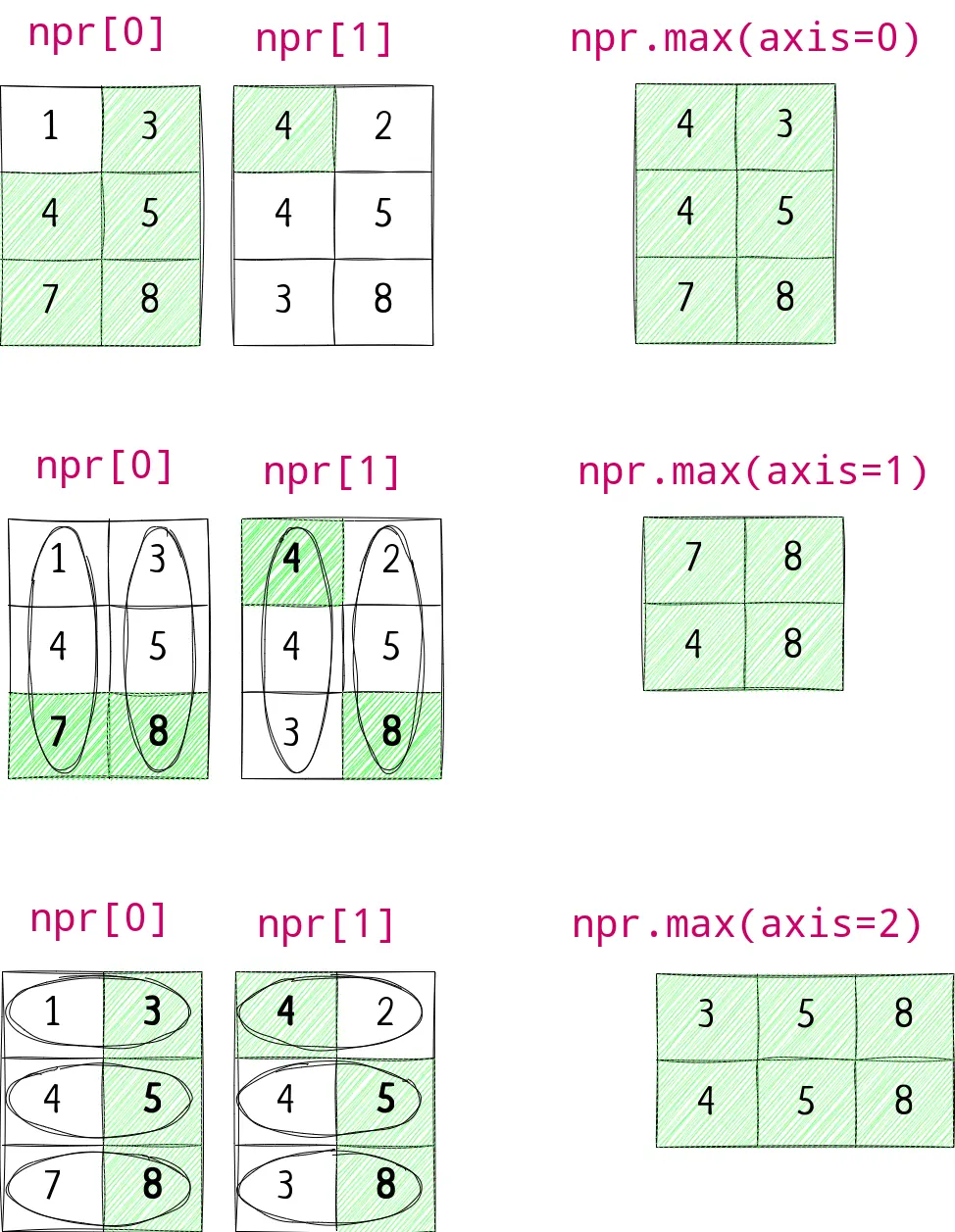
Let’s understand with one more example of max operation.
1
2
npr=np.array([1,3,4,5,7,8,4,2,4,5,3,8])
npr.reshape(2,3,2).max(axis=0)
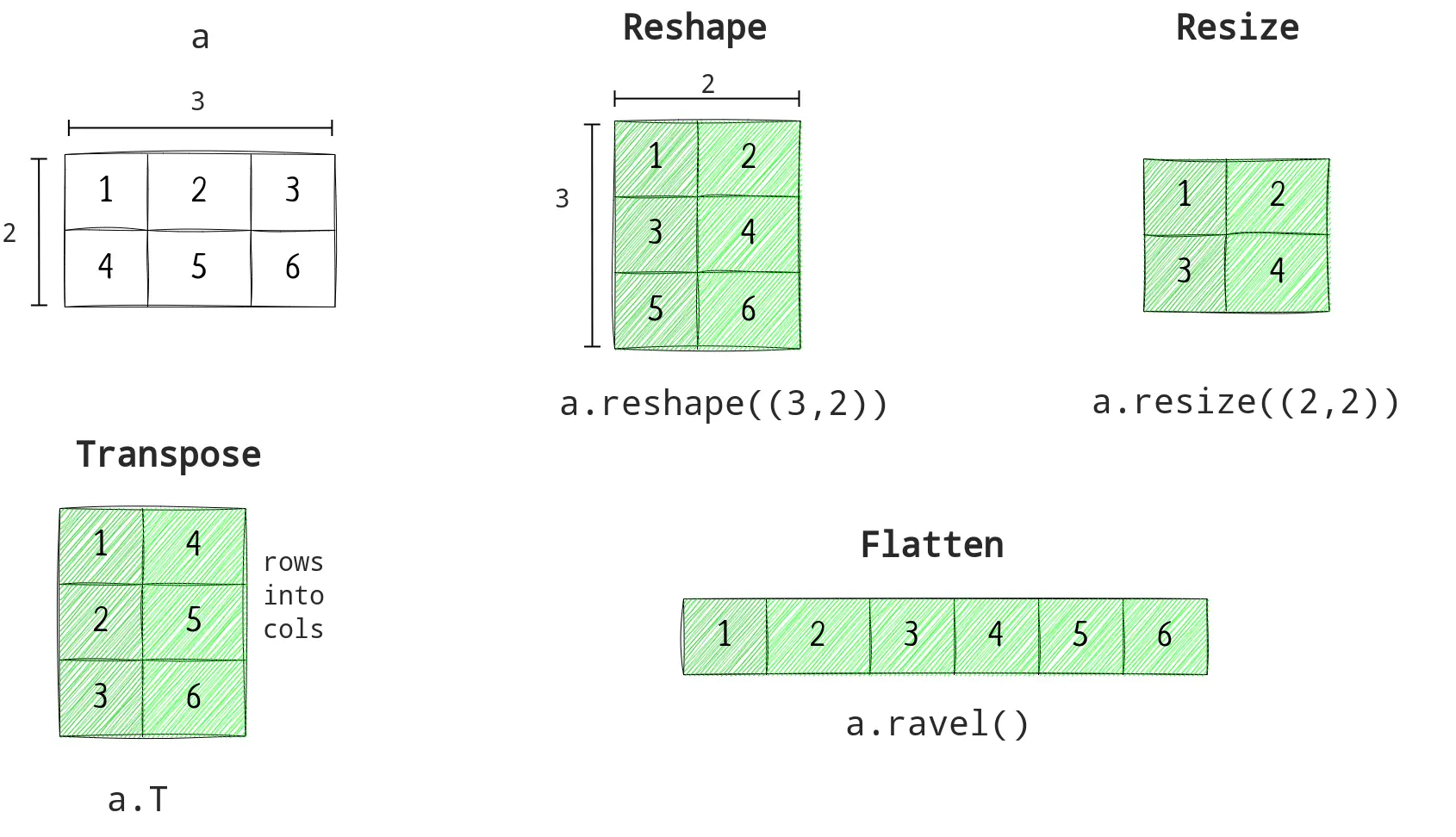
Restructure
Remember that each dimension should have same number of elements.
- resize: Change the original array
- reshape: Returns a new array
- transpose: Rows into columns and vice versa
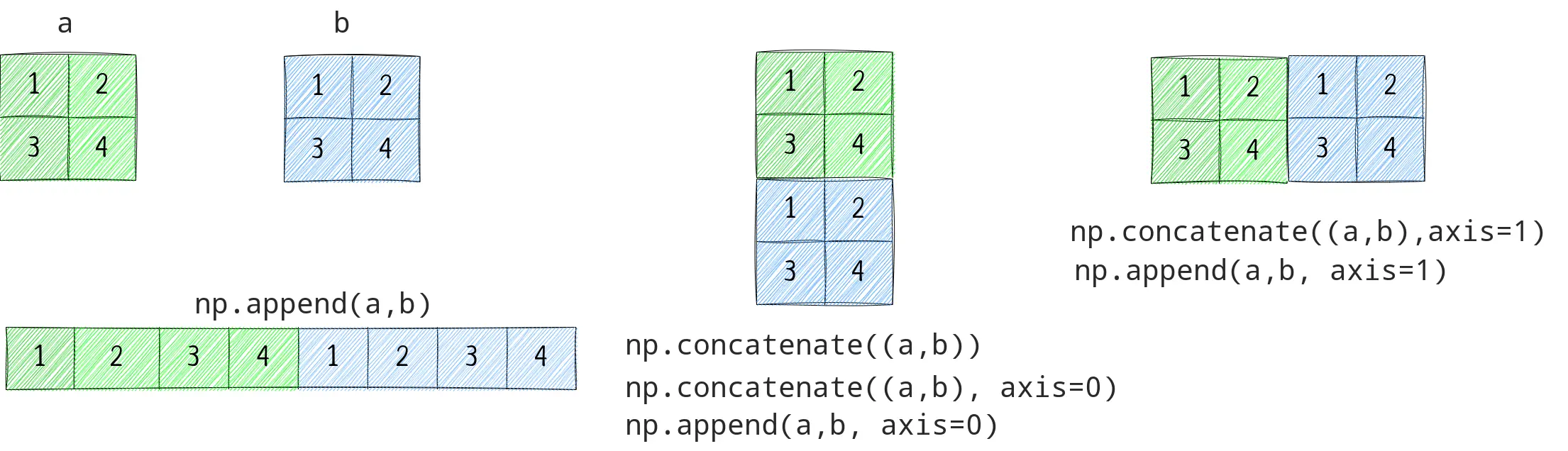
You can append or concatenate 2 arrays in following ways;
insert and delete works in the same way. For a 2d array, you can consider axis 0 as row and axis 1 as column. If you insert a single value, numpy automatically fill remaining items with the same value. Otherwise you need to take care of the size.
1
2
a = np.arange(1,10).reshape(3,3)
a = np.insert(a,1,[9,9,9],axis=0)
Output
1
2
3
4
array([[1, 2, 3],
[9, 9, 9],
[4, 5, 6],
[7, 8, 9]])
Since each row has 3 items, you can insert either 9 or [9,9,9]. any other shape will give error.
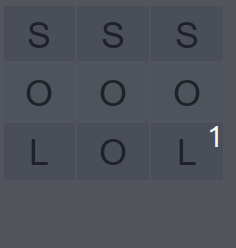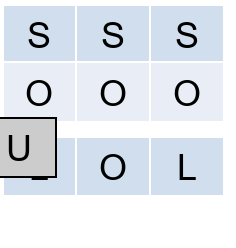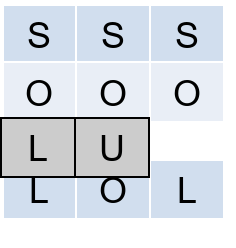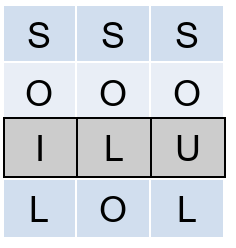

To understand delete operation, reverse the animation above.
1
2
3
4
a = np.arange(1,10).reshape(3,3)
a2 = np.insert(a,1,[9,9,9],axis=0)
a3 = np.delete(a2,1,axis=0)
a == a3
Output
1
2
3
array([[ True, True, True],
[ True, True, True],
[ True, True, True]])
If you want single value output
1
np.array_equal(a,a3) # True
Sort operation can also be performed on whole array or only on particular axis.
1
2
a.sort()
a2.sort(axis=0)
Advance Selection
Values from NumPy array can be selected by passing truth values array.
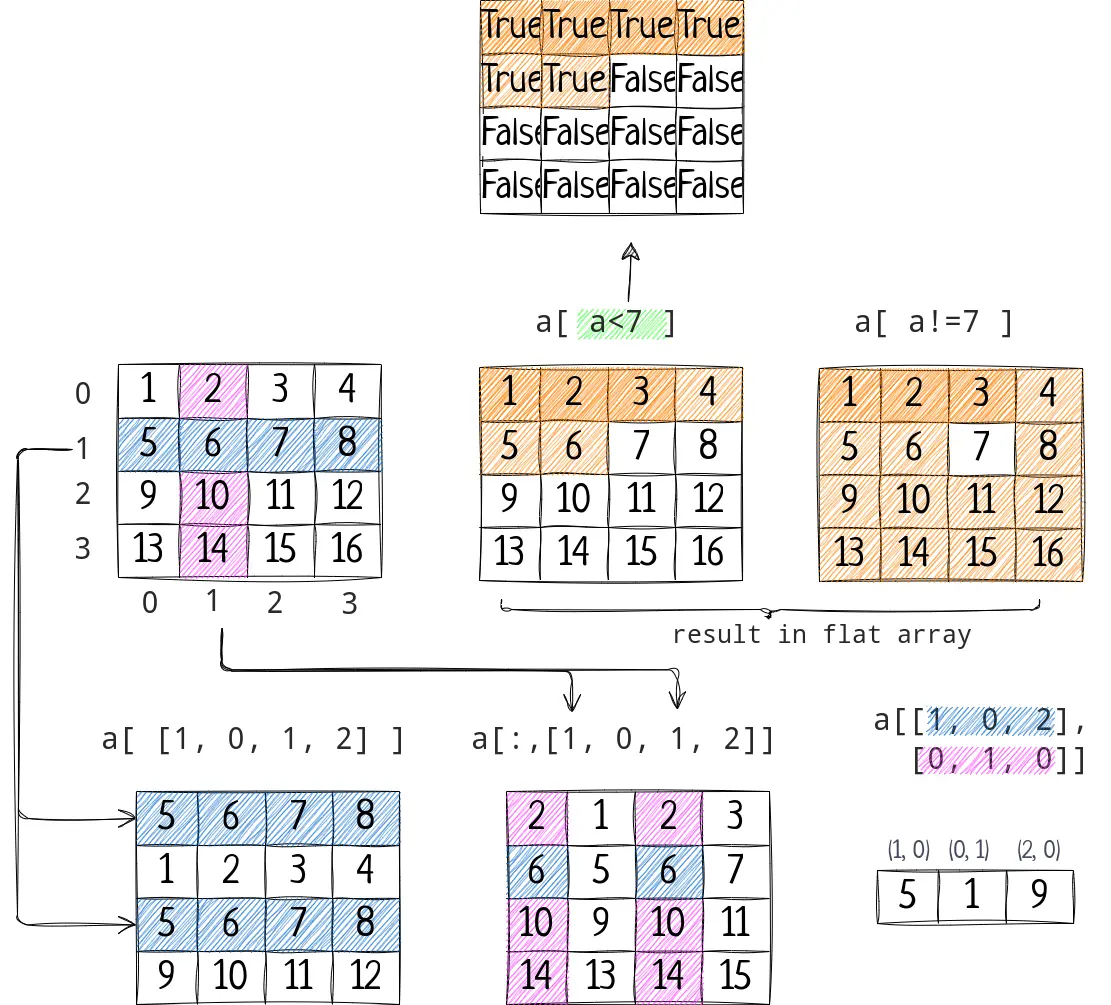
Clone
- Deep copy:
b = a[:]orb = a.copy() - View:
b = a.view(). Any change in b will reflect on a other than change in shape - Shallow copy (or reference):
b = a.
NumPy has many useful functions that reduce a lot of effort of managing and manipulating data. What you need to understand is
- Direct operations
- Axis
- Selection
Once these concepts are clear, you can understand and use it’s any function easily. But still if you feel I should cover more functions, leave a message on discussion forum.
There are many other things that you can do with numpy like storing and manipulating dates, solving math expressions, matrix, loafin or saving numpy array from/to a file etc.
Your feedback is really important. So I can improve my future articles and correct what I have already published. You can also suggest if you want me to write an article on particular topic. If you really like this blog, or article, please share with others. That's the only way I can buy time to write more articles.